Цикл Отто — Otto cycle
Термодинамический цикл для поршневых двигателей с искровым зажиганием
Диаграмма давление – объем Диаграмма температура-энтропияИдеализированные диаграммы четырехтактного цикла Отто Обе диаграммы : такт впуска ( A ) выполняется изобарическим расширением, за которым следует такт адиабатического сжатия ( B ) . При сгорании топлива тепло добавляется в процессе постоянного объема ( изохорный процесс ), за которым следует такт мощности процесса адиабатического расширения ( C ) . Цикл замыкается тактом выпуска ( D ) , характеризующимся изохорным охлаждением и изоэнтропическим сжатием.
Отто цикл представляет собой идеализированный термодинамический цикл , который описывает функционирование типичного искрового зажигания поршневых двигателей внутреннего сгорания . Это термодинамический цикл, наиболее часто встречающийся в автомобильных двигателях.
Цикл Отто — это описание того, что происходит с массой газа, когда она подвергается изменениям давления, температуры, объема, добавления тепла и отвода тепла.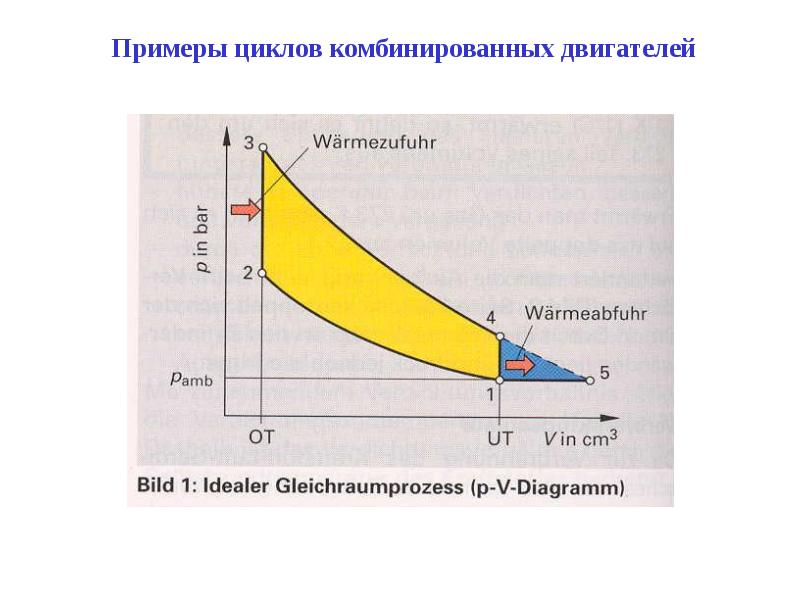
Цикл Отто состоит из:
- Верх и низ петли: пара квазипараллельных и изоэнтропических процессов (без трения, адиабатический обратимый).
- Левая и правая стороны петли: пара параллельных изохорных отростков (постоянный объем).
Изэнтропический процесс сжатия или расширения подразумевает, что не будет неэффективности (потери механической энергии) и не будет передачи тепла в систему или из нее во время этого процесса. Предполагается, что цилиндр и поршень в это время не пропускают тепло. Работа над системой выполняется во время процесса нижнего изоэнтропического сжатия.
Процессы
Процессы описываются:
- Процесс 0–1: масса воздуха всасывается в поршень / цилиндр при постоянном давлении.
- Процесс 1–2 представляет собой адиабатическое (изэнтропическое) сжатие заряда по мере того, как поршень перемещается от нижней мертвой точки ( НМТ ) к верхней мертвой точке
- Процесс 2–3 — это передача тепла рабочему газу с постоянным объемом от внешнего источника, когда поршень находится в верхней мертвой точке. Этот процесс представляет собой воспламенение топливно-воздушной смеси и последующее быстрое горение.
- Процесс 3–4 представляет собой адиабатическое (изэнтропическое) расширение (рабочий ход).

- Процесс 4–1 завершает цикл процессом с постоянным объемом, в котором тепло отводится от воздуха, когда поршень находится в нижней мертвой точке.
- Процесс 1–0: масса воздуха выбрасывается в атмосферу при постоянном давлении.
Цикл Отто состоит из изоэнтропического сжатия, добавления тепла при постоянном объеме, изэнтропического расширения и отвода тепла при постоянном объеме. В случае четырехтактного цикла Отто технически существует два дополнительных процесса: один для отвода отработанного тепла и продуктов сгорания при постоянном давлении (изобарический), а другой для впуска холодного, богатого кислородом воздуха также при постоянном давлении. ; однако в упрощенном анализе они часто опускаются. Несмотря на то, что эти два процесса имеют решающее значение для функционирования реального двигателя, в котором важны детали теплопередачи и химии сгорания, для упрощенного анализа термодинамического цикла удобнее предположить, что все отходящее тепло является удаляется при однократном изменении громкости.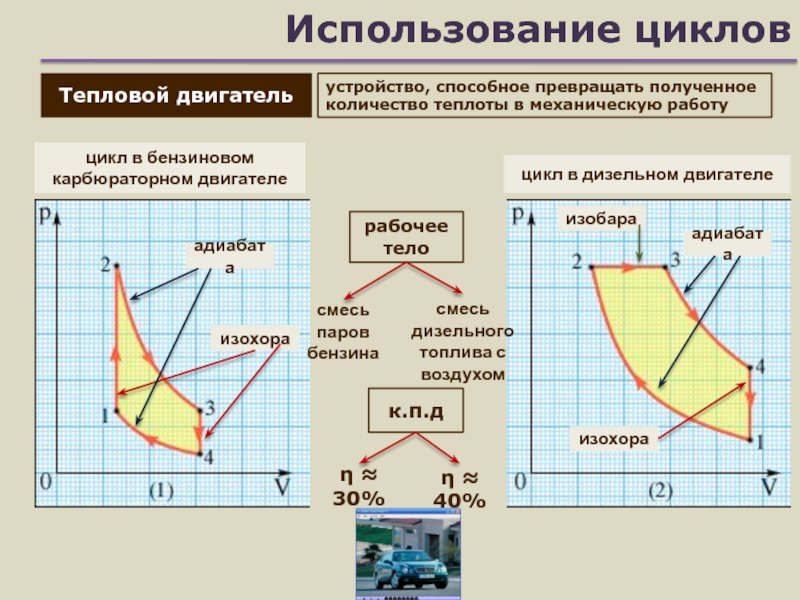
История
Четырехтактный двигатель был впервые запатентован Альфонсом Бо де Роша в 1861 году. Ранее, примерно в 1854–1857 годах, два итальянца ( Эудженио Барсанти и Феличе Маттеуччи ) изобрели двигатель, который, по слухам, был очень похож, но патент был утерян.
Первым, кто построил рабочий четырехтактный двигатель, стационарный двигатель, использующий в качестве топлива смесь угля и воздуха ( газовый двигатель ), был немецкий инженер Николаус Отто . Вот почему четырехтактный принцип сегодня широко известен как цикл Отто, а четырехтактные двигатели, использующие свечи зажигания, часто называют двигателями Отто.
Процессы
Система определяется как масса воздуха, который втягивается из атмосферы в цилиндр, сжимается поршнем, нагревается искровым зажиганием добавленного топлива, расширяется, когда он толкает поршень, и, наконец, выходит обратно в цилиндр. Атмосфера. За массой воздуха следят по изменению его объема, давления и температуры во время различных термодинамических этапов.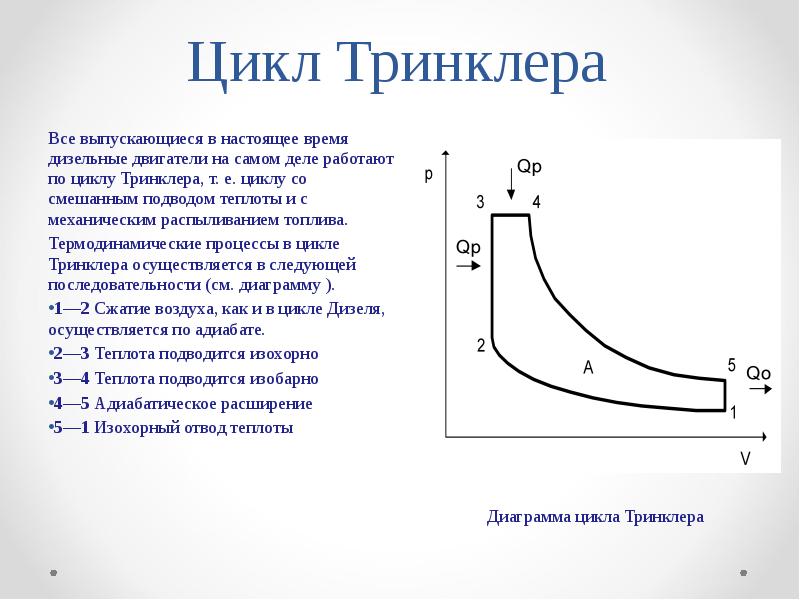 Поскольку поршень может перемещаться по цилиндру, объем воздуха изменяется в зависимости от его положения в цилиндре. Процессы сжатия и расширения, вызываемые движением поршня в газе, идеализируются как обратимые, т. Е. Никакая полезная работа не теряется из-за турбулентности или трения, и во время этих двух процессов тепло не передается газу или от него. Энергия добавляется к воздуху за счет сгорания топлива. Полезная работа извлекается за счет расширения газа в баллоне. После завершения расширения в цилиндре остающееся тепло отводится и, наконец, газ выбрасывается в окружающую среду. В процессе расширения производится полезная механическая работа, а часть этой работы используется для сжатия воздушной массы в следующем цикле. Полезная механическая работа, произведенная минусом, которая используется для процесса сжатия, — это полученная чистая работа, которую можно использовать для приведения в движение или для привода других машин. В качестве альтернативы полученная полезная работа представляет собой разницу между добавленным и удаленным теплом.
Поскольку поршень может перемещаться по цилиндру, объем воздуха изменяется в зависимости от его положения в цилиндре. Процессы сжатия и расширения, вызываемые движением поршня в газе, идеализируются как обратимые, т. Е. Никакая полезная работа не теряется из-за турбулентности или трения, и во время этих двух процессов тепло не передается газу или от него. Энергия добавляется к воздуху за счет сгорания топлива. Полезная работа извлекается за счет расширения газа в баллоне. После завершения расширения в цилиндре остающееся тепло отводится и, наконец, газ выбрасывается в окружающую среду. В процессе расширения производится полезная механическая работа, а часть этой работы используется для сжатия воздушной массы в следующем цикле. Полезная механическая работа, произведенная минусом, которая используется для процесса сжатия, — это полученная чистая работа, которую можно использовать для приведения в движение или для привода других машин. В качестве альтернативы полученная полезная работа представляет собой разницу между добавленным и удаленным теплом.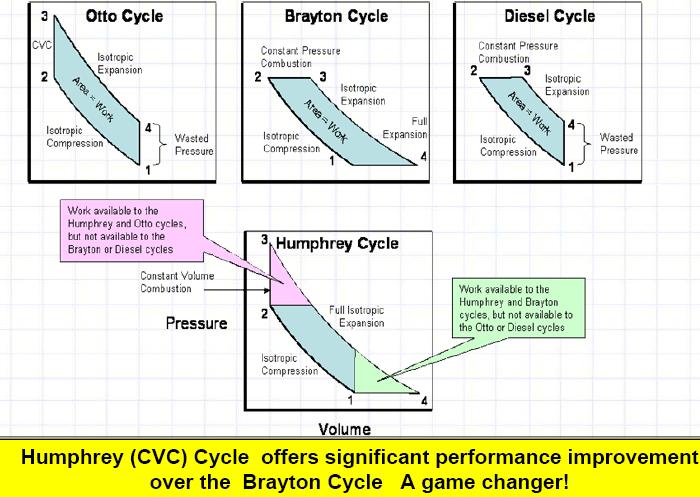
Процесс впуска 0–1 (синий оттенок)
Масса воздуха (рабочего тела) втягивается в цилиндр от 0 до 1 при атмосферном давлении (постоянное давление) через открытый впускной клапан, в то время как выпускной клапан во время этого процесса закрыт. Впускной клапан закрывается в точке 1.
Процесс 1–2 такта сжатия ( B на диаграммах)
Поршень движется от конца кривошипа (НМТ, нижняя мертвая точка и максимальный объем) к концу головки блока цилиндров ( ВМТ , верхняя мертвая точка и минимальный объем), поскольку рабочий газ с начальным состоянием 1 сжимается изоэнтропически до точки состояния 2 за счет степени сжатия ( V 1 / V 2 ) . Механически это изоэнтропическое сжатие топливовоздушной смеси в цилиндре, также известное как такт сжатия. Этот изэнтропический процесс предполагает, что механическая энергия не теряется из-за трения и тепло не передается газу или от него, следовательно, процесс обратим. Процесс сжатия требует добавления механической работы к рабочему газу.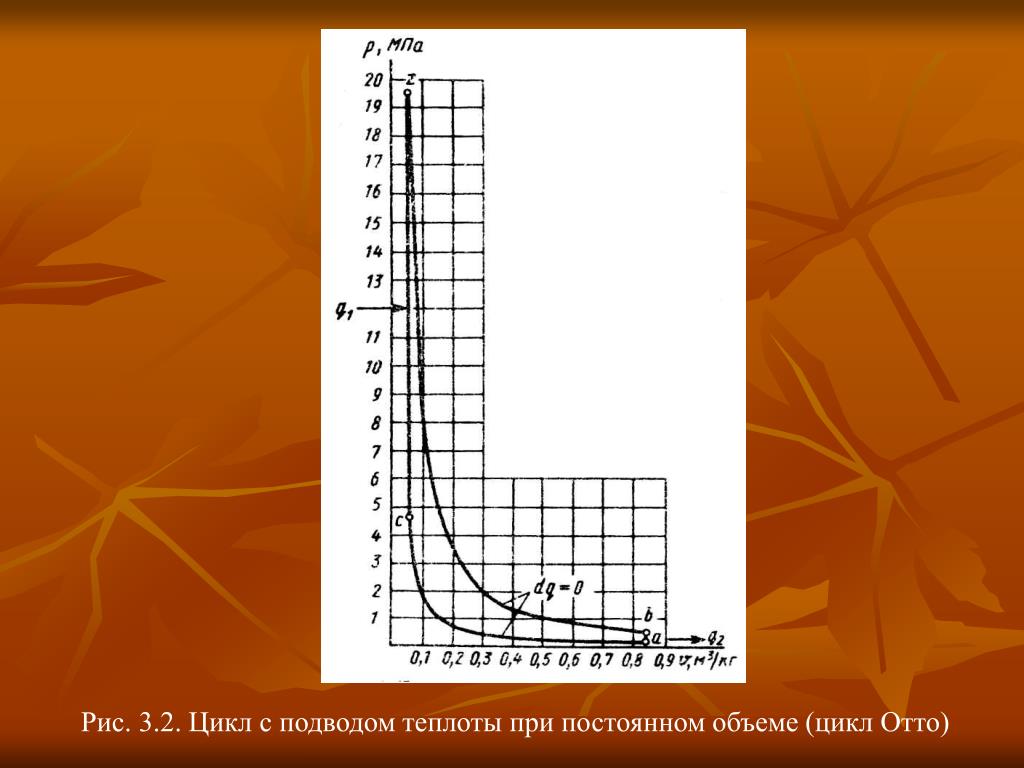
Процесс 2–3 фазы розжига ( C на диаграммах)
Поршень на мгновение находится в состоянии покоя в ВМТ . В этот момент, который известен как фаза зажигания, топливно-воздушная смесь остается в небольшом объеме в верхней части такта сжатия. Тепло добавляется к рабочему телу за счет сгорания впрыскиваемого топлива, при этом объем по существу остается постоянным. Давление повышается, и это соотношение называется «степенью взрываемости». (п3/п2){\ displaystyle (P_ {3} / P_ {2})}
Процесс 3–4 хода расширения ( D на схемах)
Повышенное высокое давление оказывает давление на поршень и толкает его к НМТ . Расширение рабочей жидкости происходит изоэнтропически и работа совершается системой на поршне. Объемный коэффициент называется «степенью изоэнтропического расширения». (Для цикла Отто такая же степень сжатия ). С механической точки зрения это расширение горячей газовой смеси в цилиндре, известное как рабочий ход (рабочий ход). V4/V3{\ displaystyle V_ {4} / V_ {3}}V1/V2{\ Displaystyle V_ {1} / V_ {2}}
Процесс 4–1 идеализированного отвода тепла ( A на диаграммах)
Поршень на мгновение находится в состоянии покоя в НМТ . Давление рабочего газа мгновенно падает от точки 4 до точки 1 во время процесса постоянного объема, поскольку тепло отводится к идеализированному внешнему поглотителю, который контактирует с головкой блока цилиндров. В современных двигателях внутреннего сгорания радиатором может быть окружающий воздух (для двигателей малой мощности) или циркулирующая жидкость, например хладагент. Газ вернулся в состояние 1.
Процесс 1–0 такта выпуска
Выпускной клапан открывается в точке 1. По мере того как поршень перемещается из «НМТ» (точка 1) в «ВМТ» (точка 0) при открытом выпускном клапане, газовая смесь сбрасывается в атмосферу, и процесс начинается заново.
Анализ цикла
В процессе 1–2 поршень действительно воздействует на газ, а в процессе 3–4 газ действительно воздействует на поршень во время этих изоэнтропических процессов сжатия и расширения, соответственно. Процессы 2–3 и 4–1 — изохорные процессы; тепло передается в систему от 2–3 и из системы от 4–1, но во время этих процессов в системе не выполняется никакой работы и не извлекается из системы. Никакая работа не выполняется во время изохорного (постоянного объема) процесса, потому что добавление или удаление работы из системы требует перемещения границ системы; следовательно, поскольку объем цилиндра не изменяется, работа вала не добавляется или не удаляется из системы.
Для описания этих четырех процессов используются четыре разных уравнения. Для упрощения предполагается, что изменениями кинетической и потенциальной энергии, которые имеют место в системе (масса газа), можно пренебречь, а затем применить первый закон термодинамики (сохранение энергии) к массе газа, когда он меняет состояние, как описано по температуре, давлению и объему газа.
Во время полного цикла газ возвращается в исходное состояние температуры, давления и объема, следовательно, чистое изменение внутренней энергии системы (газа) равно нулю. В результате энергия (тепло или работа), добавляемая к системе, должна компенсироваться энергией (теплом или работой), которая покидает систему. При анализе термодинамических систем принято считать энергию, поступающую в систему, как положительную, а энергию, покидающую систему, как отрицательную.
Уравнение 1а.
Во время полного цикла чистое изменение энергии системы равно нулю:
- ΔEзнак равноEв-Eвнезнак равно0{\ displaystyle \ Delta E = E _ {\ text {in}} — E _ {\ text {out}} = 0}
Выше указано, что система (масса газа) возвращается в исходное термодинамическое состояние, в котором она находилась в начале цикла.
Где энергия, добавленная к системе от 1–2–3, и энергия, удаленная из системы от 3–4–1. С точки зрения работы и добавленного тепла в систему Eв{\ displaystyle E _ {\ text {in}}}Eвне{\ displaystyle E _ {\ text {out}}}
Уравнение 1b:
- W1-2+Q2-3+W3-4+Q4-1знак равно0{\ displaystyle W_ {1-2} + Q_ {2-3} + W_ {3-4} + Q_ {4-1} = 0}
Каждый член уравнения может быть выражен через внутреннюю энергию газа в каждой точке процесса:
- W1-2знак равноU2-U1{\ displaystyle W_ {1-2} = U_ {2} -U_ {1}}
- Q2-3знак равноU3-U2{\ displaystyle Q_ {2-3} = U_ {3} -U_ {2}}
- W3-4знак равноU4-U3{\ displaystyle W_ {3-4} = U_ {4} -U_ {3}}
- Q4-1знак равноU1-U4{\ displaystyle Q_ {4-1} = U_ {1} -U_ {4}}
Уравнение баланса энергии 1b становится
- W1-2+Q2-3+W3-4+Q4-1знак равно(U2-U1)+(U3-U2)+(U4-U3)+(U1-U4)знак равно0{\ displaystyle W_ {1-2} + Q_ {2-3} + W_ {3-4} + Q_ {4-1} = \ left (U_ {2} -U_ {1} \ right) + \ left ( U_ {3} -U_ {2} \ right) + \ left (U_ {4} -U_ {3} \ right) + \ left (U_ {1} -U_ {4} \ right) = 0}
Чтобы проиллюстрировать пример, мы выбираем некоторые значения для точек на иллюстрации:
- U1знак равно1{\ displaystyle U_ {1} = 1}
- U2знак равно5{\ displaystyle U_ {2} = 5}
- U3знак равно9{\ displaystyle U_ {3} = 9}
- U4знак равно4{\ displaystyle U_ {4} = 4}
Эти значения выбраны произвольно, но рационально. Затем можно рассчитать сроки работы и тепла.
Энергия, добавленная к системе в качестве работы при сжатии от 1 до 2, равна
- (U2-U1)знак равно(5-1)знак равно4{\ displaystyle \ left (U_ {2} -U_ {1} \ right) = \ left (5-1 \ right) = 4}
Энергия, добавленная к системе в виде тепла от точки 2 до 3, равна
- (U3-U2)знак равно(9-5)знак равно4{\ displaystyle \ left ({U_ {3} -U_ {2}} \ right) = \ left (9-5 \ right) = 4}
Энергия, удаляемая из системы в качестве работы при расширении с 3 до 4, составляет
- (U4-U3)знак равно(4-9)знак равно-5{\ Displaystyle \ left (U_ {4} -U_ {3} \ right) = \ left (4-9 \ right) = — 5}
Энергия, удаляемая из системы в виде тепла от точки 4 до 1, равна
- (U1-U4)знак равно(1-4)знак равно-3{\ displaystyle \ left (U_ {1} -U_ {4} \ right) = \ left (1-4 \ right) = — 3}
Энергетический баланс
- ΔEзнак равно+4+4-5-3знак равно0{\ displaystyle \ Delta E = + 4 + 4-5-3 = 0}
Обратите внимание, что энергия, добавленная в систему, считается положительной, а энергия, выходящая из системы, считается отрицательной, а сумма, как и ожидалось, равна нулю для полного цикла, который возвращает систему в исходное состояние.
Исходя из энергетического баланса работа системы составляет:
- ∑работайзнак равноW1-2+W3-4знак равно(U2-U1)+(U4-U3)знак равно4-5знак равно-1{\ displaystyle \ sum {\ text {Work}} = W_ {1-2} + W_ {3-4} = \ left (U_ {2} -U_ {1} \ right) + \ left (U_ {4} -U_ {3} \ right) = 4-5 = -1}
Чистая энергия, выходящая из системы в виде работы, равна -1, что означает, что система произвела одну чистую единицу энергии, которая покидает систему в виде работы.
Чистое тепло, выходящее из системы:
- ∑Высокая температуразнак равноQ2-3+Q4-1знак равно(U3-U2)+(U1-U4)знак равно4-3знак равно1{\ displaystyle \ sum {\ text {Heat}} = Q_ {2-3} + Q_ {4-1} = \ left (U_ {3} -U_ {2} \ right) + \ left (U_ {1} -U_ {4} \ right) = 4-3 = 1}
Как энергия, добавленная в систему, так и тепло положительно. Из вышесказанного кажется, что система получила одну единицу тепла. Это соответствует энергии, производимой системой, как работе системы.
Тепловая эффективность — это отношение чистой работы системы к теплу, добавленному в систему. Уравнение 2:
- ηзнак равноW1-2+W3-4Q2-3знак равно(U2-U1)+(U4-U3)(U3-U2){\ displaystyle \ eta = {\ frac {W_ {1-2} + W_ {3-4}} {Q_ {2-3}}} = {\ frac {\ left (U_ {2} -U_ {1}) \ right) + \ left (U_ {4} -U_ {3} \ right)} {\ left (U_ {3} -U_ {2} \ right)}}}
- ηзнак равно1+U1-U4(U3-U2)знак равно1+(1-4)(9-5)знак равно0,25{\ displaystyle \ eta = 1 + {\ frac {U_ {1} -U_ {4}} {\ left (U_ {3} -U_ {2} \ right)}} = 1 + {\ frac {(1- 4)} {(9-5)}} = 0,25}
В качестве альтернативы тепловой КПД может быть получен за счет строгого добавления тепла и отвода тепла.
- ηзнак равноQ2-3+Q4-1Q2-3знак равно1+(U1-U4)(U3-U2){\ displaystyle \ eta = {\ frac {Q_ {2-3} + Q_ {4-1}} {Q_ {2-3}}} = 1 + {\ frac {\ left (U_ {1} -U_ { 4} \ right)} {\ left (U_ {3} -U_ {2} \ right)}}}
Предоставление фиктивных ценностей
ηзнак равно1+1-49-5знак равно1+-34знак равно0,25{\ displaystyle \ eta = 1 + {\ frac {1-4} {9-5}} = 1 + {\ frac {-3} {4}} = 0,25}
В цикле Отто отсутствует теплопередача во время процессов 1–2 и 3–4, поскольку они являются изоэнтропическими процессами. Тепло подводится только во время процессов постоянного объема 2–3, а тепло отводится только во время процессов постоянного объема 4–1.
Вышеупомянутые значения являются абсолютными величинами, которые могут, например, иметь единицы измерения в джоулях (при условии, что будет использоваться система единиц MKS) и могут использоваться для конкретного двигателя с определенными размерами. При изучении термодинамических систем обширные величины, такие как энергия, объем или энтропия (по сравнению с интенсивными величинами температуры и давления), относятся к единице массы, как и вычисления, делая их более общими и, следовательно, более общими. использовать. Следовательно, каждый член, включающий экстенсивное количество, можно разделить на массу, дав такие термины, как джоуль / кг (удельная энергия), метры 3 / кг (удельный объем) или джоуль / (кельвин · кг) (удельная энтропия, тепло емкость) и т. д. и будут представлены строчными буквами, u, v, s и т. д.
Уравнение 1 теперь можно связать с уравнением теплоемкости для постоянного объема. Эти удельные теплоемкости особенно полезны для термодинамических расчетов , связанных с идеальным газом модели.
- Cvзнак равно(δтыδТ)v{\ displaystyle C _ {\ text {v}} = \ left ({\ frac {\ delta u} {\ delta T}} \ right) _ {\ text {v}}}
Переставляем урожайность:
- δтызнак равно(Cv)(δТ){\ Displaystyle \ дельта и = (С _ {\ текст {v}}) (\ дельта Т)}
Вставка уравнения теплоемкости в уравнение тепловой эффективности (уравнение 2) дает.
- ηзнак равно1-(Cv(Т4-Т1)Cv(Т3-Т2)){\ displaystyle \ eta = 1- \ left ({\ frac {C _ {\ text {v}} (T_ {4} -T_ {1})} {C _ {\ text {v}} (T_ {3} — T_ {2})}} \ right)}
При перестановке:
- ηзнак равно1-(Т1Т2)(Т4/Т1-1Т3/Т2-1){\ displaystyle \ eta = 1- \ left ({\ frac {T_ {1}} {T_ {2}}} \ right) \ left ({\ frac {T_ {4} / T_ {1} -1} { T_ {3} / T_ {2} -1}} \ right)}
Далее, учитывая диаграммы (см. Изоэнтропические соотношения для идеального газа ), оба из них могут быть опущены. Затем уравнение сводится к: Т4/Т1знак равноТ3/Т2{\ displaystyle T_ {4} / T_ {1} = T_ {3} / T_ {2}}
Уравнение 2:
- ηзнак равно1-(Т1Т2){\ displaystyle \ eta = 1- \ left ({\ frac {T_ {1}} {T_ {2}}} \ right)}
Поскольку в цикле Отто используются изэнтропические процессы во время сжатия (процессы с 1 по 2) и расширения (с 3 по 4), изоэнтропические уравнения идеальных газов и отношения постоянного давления / объема могут использоваться для получения уравнений 3 и 4. { (\ gamma -1)}}
- где
- γзнак равно(CпCv){\ displaystyle {\ gamma} = \ left ({\ frac {C _ {\ text {p}}} {C _ {\ text {v}}}} \ right)}
- γ{\ displaystyle {\ gamma}} — удельная теплоемкость
- Вывод предыдущих уравнений находится путем решения этих четырех уравнений соответственно (где — удельная газовая постоянная ):р{\ displaystyle R}
- Cппер(V1V2)-рпер(п2п1)знак равно0{\ displaystyle C _ {\ text {p}} \ ln \ left ({\ frac {V_ {1}} {V_ {2}}} \ right) -R \ ln \ left ({\ frac {p_ {2}) } {p_ {1}}} \ right) = 0}
- Cvпер(Т2Т1)-рпер(V2V1)знак равно0{\ displaystyle C _ {\ text {v}} \ ln \ left ({\ frac {T_ {2}} {T_ {1}}} \ right) -R \ ln \ left ({\ frac {V_ {2}) } {V_ {1}}} \ right) = 0}
- Cпзнак равно(γрγ-1){\ displaystyle C _ {\ text {p}} = \ left ({\ frac {\ gamma R} {\ gamma -1}} \ right)}
- Cvзнак равно(рγ-1){\ displaystyle C _ {\ text {v}} = \ left ({\ frac {R} {\ gamma -1}} \ right)}
Дальнейшее упрощение уравнения 4, где — степень сжатия : р{\ displaystyle r}(V1/V2){\ displaystyle (V_ {1} / V_ {2})}
Уравнение 5:
- (Т2Т1)знак равно(V1V2)(γ-1)знак равнор(γ-1){\ displaystyle \ left ({\ frac {T_ {2}} {T_ {1}}} \ right) = \ left ({\ frac {V_ {1}} {V_ {2}}} \ right) ^ { (\ gamma -1)} = r ^ {(\ gamma -1)}}
Обращая уравнение 4 и вставляя его в уравнение 2, конечный тепловой КПД можно выразить как:
Уравнение 6:
- ηзнак равно1-(1р(γ-1)){\ displaystyle \ eta = 1- \ left ({\ frac {1} {r ^ {(\ gamma -1)}}} \ right)}
Из анализа уравнения 6 очевидно, что КПД цикла Отто напрямую зависит от степени сжатия . Так как для воздуха 1,4, увеличение приведет к увеличению . Однако для продуктов сгорания топливовоздушной смеси часто принимают примерно 1,3. Из приведенного выше обсуждения следует, что более эффективно иметь высокую степень сжатия. Стандартное соотношение для типичных автомобилей составляет примерно 10: 1. Обычно это не сильно увеличивается из-за возможности самовоспламенения или « стука », который устанавливает верхний предел степени сжатия. В процессе сжатия 1–2 температура повышается, поэтому увеличение степени сжатия вызывает повышение температуры. Самовоспламенение происходит, когда температура топливно-воздушной смеси становится слишком высокой до того, как она воспламеняется фронтом пламени. Такт сжатия предназначен для сжатия продуктов до того, как пламя воспламенит смесь. Если степень сжатия увеличивается, смесь может самовоспламеняться до завершения такта сжатия, что приводит к «детонации двигателя». Это может повредить компоненты двигателя и снизить тормозную мощность двигателя. р{\ displaystyle r}γ{\ displaystyle \ gamma}р{\ displaystyle r}η{\ displaystyle \ eta}γ{\ displaystyle \ gamma}
Мощность
Энергия, производимая циклом Отто, — это энергия, вырабатываемая в единицу времени. Двигатели Отто называются четырехтактными. Такт впуска и такт сжатия требуют одного оборота коленчатого вала двигателя. Рабочий ход и такт выпуска требуют еще одного поворота. На два оборота приходится один рабочий ход.
Из приведенного выше анализа цикла чистая работа, произведенная системой:
- ∑ работайзнак равноW1-2+W3-4знак равно(U2-U1)+(U4-U3)знак равно+4-5знак равно-1{\ displaystyle \ sum {\ text {Work}} = W_ {1-2} + W_ {3-4} = \ left (U_ {2} -U_ {1} \ right) + \ left (U_ {4} -U_ {3} \ right) = + 4-5 = -1}
(опять же, используя соглашение о знаках, знак минус означает, что энергия покидает систему в качестве работы)
Если бы используемые единицы были MKS, цикл произвел бы один джоуль энергии в форме работы. Для двигателя определенного рабочего объема, например одного литра, масса газа в системе может быть рассчитана, если двигатель работает при стандартной температуре (20 ° C) и давлении (1 атм). Согласно универсальному закону газа, масса одного литра газа находится при комнатной температуре и давлении на уровне моря:
- Mзнак равнопVрТ{\ displaystyle M = {\ frac {PV} {RT}}}
- V = 0,001 м 3 , R = 0,286 кДж / (кг · К), T = 293 K, P = 101,3 кН / м 2
- M = 0,00121 кг
При частоте вращения двигателя 3000 об / мин происходит 1500 рабочих ходов в минуту или 25 рабочих ходов в секунду.
- ∑ работайзнак равно1J/(кг⋅инсульт)×0,00121кгзнак равно0,00121J/инсульт{\ displaystyle \ sum {\ text {Work}} = 1 \, {\ text {J}} / ({\ text {kg}} \ cdot {\ text {stroke}}) \ times 0.00121 \, {\ text {kg}} = 0,00121 \, {\ text {J}} / {\ text {stroke}}}
Мощность в 25 раз больше, так как 25 рабочих ходов в секунду
- пзнак равно25×0,00121знак равно0,0303J/sилиW{\ displaystyle P = 25 \ times 0,00121 = 0,0303 \, {\ text {J}} / {\ text {s}} \; {\ text {или}} \; {\ text {W}}}
Если двигатель многоцилиндровый, результат умножается на этот коэффициент. Если каждый цилиндр имеет разный литражный объем, результаты также умножаются на этот коэффициент. Эти результаты являются произведением значений внутренней энергии, которые были приняты для четырех состояний системы в конце каждого из четырех тактов (два вращения). Они были выбраны только для иллюстрации и, очевидно, имеют низкую ценность. Замена фактических значений из реального двигателя приведет к результатам, близким к результатам двигателя. Чьи результаты будут выше, чем у реального двигателя, поскольку в анализе сделано много упрощающих допущений, которые не учитывают неэффективность. Такие результаты привели бы к завышению выходной мощности.
Повышение мощности и эффективности
Разница между давлением и температурами выхлопа и впуска означает, что некоторое повышение эффективности может быть достигнуто за счет использования турбонагнетателя, удаления из потока выхлопных газов некоторой части оставшейся энергии и передачи ее во впускной поток для увеличения давления на впуске. Газовая турбина может извлекать полезную рабочую энергию из выхлопного потока, которая затем может использоваться для повышения давления всасываемого воздуха. Давление и температура выхлопных газов будут уменьшаться, поскольку они расширяются через газовую турбину, и эта работа затем применяется к потоку всасываемого газа, увеличивая его давление и температуру. Передача энергии приводит к повышению эффективности, а результирующая удельная мощность двигателя также улучшается. Впускной воздух обычно охлаждается, чтобы уменьшить его объем, поскольку работа, производимая за один ход, является прямой функцией количества массы, принимаемой в цилиндр; более плотный воздух будет производить больше работы за цикл. Фактически, температура всасываемого воздуха также должна быть снижена, чтобы предотвратить преждевременное возгорание в двигателе, работающем на бензине; следовательно, промежуточный охладитель используется для отвода некоторой энергии в виде тепла и, таким образом, снижения температуры на входе. Такая схема увеличивает как КПД, так и мощность двигателя.
Применение нагнетателя, приводимого в действие коленчатым валом, действительно увеличивает выходную мощность (удельную мощность), но не увеличивает эффективность, поскольку он использует некоторую чистую работу, производимую двигателем для повышения давления всасываемого воздуха, и не может извлечь в противном случае потерянную энергию, связанную с поток выхлопных газов при высокой температуре и давлении в окружающую среду.
Ссылки
Цикл Отто — Студопедия
идеальным газом, где Ср=f(t) и анимацией фаз (pic) http://twt.mpei.ac.ru/MAS/Worksheets/Therm/Otto_anim.mcd |
Цикл Отто — термодинамический цикл, описывающий рабочий процесс двигателя внутреннего сгорания с воспламенением сжатой смеси от постороннего источника энергии, цикл бензинового двигателя. Назван в честь немецкого инженера Николауса Отто.
Идеальный цикл Отто состоит из четырёх процессов:
p-V диаграмма цикла Отто
· 1—2 адиабатное сжатие рабочего тела;
· 2—3 изохорный подвод теплоты к рабочему телу;
· 3—4 адиабатное расширение рабочего тела;
· 4—1 изохорное охлаждение рабочего тела.
КПД цикла Отто ,
где — степень сжатия,
— показатель адиабаты.
Идеальный цикл лишь приблизительно описывает процессы, происходящие в реальном двигателе, но для технических расчётов в большинстве случаев точность такого приближения удовлетворительна.
Цикл Карно(описание в Википедии)
для идеального газа (pic) MAS 11 MCS 14
для идеального газа с Ср=f(t) (pic) http://twt.mpei.ac.ru/MAS/Worksheets/Therm/carno_Cp_T.mcd
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.
Цикл Карно назван в честь французского военного инженера Сади Карно, который впервые его исследовал в 1824 году.
Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.
Цикл Отто — Википедия
| Термодинамические циклы | |||||||
|---|---|---|---|---|---|---|---|
| Статья является частью серии «Термодинамика». | |||||||
| Эталонный цикл Эдвардса | |||||||
| Цикл Аткинсона | |||||||
| Цикл Брайтона/Джоуля | |||||||
| Цикл Гирна | |||||||
| Цикл Дизеля | |||||||
| Цикл Калины | |||||||
| Цикл Карно | |||||||
| Цикл Ленуара | |||||||
| Цикл Миллера | |||||||
| Цикл Отто | |||||||
| Цикл Ренкина | |||||||
| Цикл Стирлинга | |||||||
| Цикл Тринклера | |||||||
| Цикл Хамфри | |||||||
| Цикл Эрикссона | |||||||
| Разделы термодинамики | |||||||
| Начала термодинамики | |||||||
| Уравнение состояния | |||||||
| Термодинамические величины | |||||||
| Термодинамические потенциалы | |||||||
| Термодинамические циклы | |||||||
| Фазовые переходы | |||||||
| править | |||||||
| См.{k-1}}}}, где n=V1/V2{\displaystyle n=V_{1}/V_{2}} — степень сжатия,
Идеальный цикл лишь приблизительно описывает процессы, происходящие в реальном двигателе, но для технических расчётов в большинстве случаев точность такого приближения удовлетворительна. См. также
Ссылки
Термодинамические циклы — ВикипедияТермодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура и энтропия). Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела). Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, цикл Стирлинга и цикл Эрикссона (англ.)), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора. Общим (т.е. указанные циклы частный случай) для всех этих циклов с регенерацией является Цикл Рейтлингера. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью. Основные принципыПрямое преобразование тепловой энергии в работу запрещается постулатом Томсона (см. Второе начало термодинамики). Поэтому для этой цели используются термодинамические циклы. Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты (Q1{\displaystyle Q_{1}}) у нагревателя и отдаёт количество теплоты Q2{\displaystyle Q_{2}} холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом,
так как изменение внутренней энергии U{\displaystyle U} в круговом процессе равно нулю (это функция состояния). Напомним, что работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю. При этом нагреватель потратил энергию Q1{\displaystyle Q_{1}}. Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен
Вычисление работы и КПД в термодинамическом циклеРабота в термодинамическом цикле, по определению, равна
где C{\displaystyle C} — контур цикла. C другой стороны, в соответствии с первым началом термодинамики, можно записать
Аналогичным образом, количество теплоты, переданное нагревателем рабочему телу, равно
Отсюда видно, что наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия. Цикл Карно и максимальный КПД тепловой машиныОсновная статья: Цикл Карно. Цикл Карно в координатах T и SПредставим себе следующий цикл: Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу Q1=TH(S2−S1){\displaystyle Q_{1}=T_{H}(S_{2}-S_{1})} тепла в изотермическом процессе (при постоянной температуре), при этом объём рабочего тела увеличивается. Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически (без теплообмена с окружающей средой). При этом его температура уменьшается до температуры холодильника. Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему Q2=TX(S2−S1){\displaystyle Q_{2}=T_{X}(S_{2}-S_{1})} тепла в изотермическом процессе. При этом объём рабочего тела уменьшается. Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя. Его КПД равен, таким образом,
то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо. Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД. Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно. См. такжеСсылкиЛитература
Идеальные циклы поршневых двигателей внутреннего сгорания.Идеальные циклы поршневых двигателейПонятие о цикле двигателя внутреннего сгоранияПоследовательность термодинамических процессов в любом современном поршневом двигателе внутреннего сгорания в той или иной степени приближена к одному из трех характерных циклов, называемых идеальными циклами Отто, Дизеля и Сабатэ – Тринклера (Сабатье – Тринклера). Исходя из приведенных характеристик, циклы Отто, Дизеля и Сабатэ – Тринклера иногда называют, соответственно, циклами быстрого, постоянного и смешанного сгорания, которые положены в основу работы карбюраторного, компрессорного и бескомпрессорного двигателей. Приведенные ниже идеальные циклы тепловых двигателей внутреннего сгорания описывают последовательность термодинамических процессов, протекающие по двухтактному сценарию, т. е. поршень в цилиндре совершает за один цикл два хода — вверх и вниз. Реальные тепловые двигатели могут работать и по двухтактному, и по более эффективному четырехтактному циклу. *** Цикл ОттоИдеальный цикл теплового двигателя внутреннего сгорания с принудительным воспламенением горючей смеси, который обычно называют циклом Отто, на самом деле был описан и предложен еще в 1862 году французским инженером Альфонсом Бо Де Роша (1815-1891), т. е. задолго до создания Николаусом Августом Отто своего знаменитого двигателя, первый образец которого был изготовлен спустя полтора десятилетия — в 1878 году. Поэтому заслуга Отто заключается лишь в осуществлении указанного цикла на практике. В своем двигателе Отто первым применил сжатие рабочей смеси для поднятия максимальной температуры цикла, которое осуществлялось по адиабате (т. е. без теплообмена с внешней средой). Последовательность термодинамических процессов в цикле Отто можно проследить по приведенной ниже диаграмме (рис. 1). Далее следовало адиабатическое расширение, в процессе которого двигателем осуществлялась полезная работа (рабочий ход поршня). В конце процесса расширения следовал изохорный отвод теплоты (открывание клапанов и продувание цилиндра). На этом цикл завершался, после чего следовало повторение указанной последовательности процессов, составляющих череду аналогичных циклов. Как указывалось выше, А. Отто первым применил сжатие рабочей смеси перед воспламенением, благодаря чему КПД его двигателя значительно превышал КПД двигателя Э. Ленуара, в котором сжатие не предусматривалось. Современные двигатели, работающие по схеме цикла Отто, имеют степень сжатия (в зависимости от конструктивных особенностей) от 8 до 12,5. По такому циклу работают двигатели с принудительным воспламенением горючей смеси, использующие в качестве топлива бензин или газ. Из-за относительно невысокой степени сжатия горючей смеси в цилиндрах, термический КПД таких двигателей ниже, чем в дизельных двигателях, и достигает 30-35 %. Двигатели, работающие по циклу Отто, в настоящее время широко применяются в автомобилях, лодочных моторах, маломощных летательных аппаратах и т. п. *** Цикл ДизеляДругой характерный идеальный цикл для ДВС называют циклом Дизеля, по имени изобретателя дизельного двигателя. Этот цикл характеризуется подводом теплоты (сгоранием топлива) по изобаре, т. е. при постоянном давлении в цилиндре двигателя. Как и в случае с циклом Отто, называть цикл, в котором сгорание топлива осуществляется по изобаре, циклом Дизеля будет не совсем справедливо. Цикл Дизеля протекает по следующему сценарию (см. диаграмму на рис. 1). Принципиальное и конструктивное отличие заключалось в том, что Дизель предложил сжимать в цилиндре не топливовоздушную смесь, как в двигателях Отто, а воздух. В конце такта сжатия температура воздуха поднималась настолько, что впрыскиваемое в цилиндр топливо возгоралось самостоятельно, т. е. происходило самовоспламенение топлива. По легенде считается, что Р. Дизель изобрел свой знаменитый двигатель, накачивая ручным насосом колесо велосипеда. После нескольких энергичных манипуляций насосом, он заметил, что его корпус-цилиндр сильно нагрелся, и даже обжигал руку. Это и натолкнуло изобретателя на идею, которая принесла ему мировую славу и бессмертие в памяти благодарного человечества. Особенностью системы питания Дизеля, в его первозданном виде, было компрессорное пневматическое распыливание топлива, на смену которому со временем пришло механическое распыливание посредством топливных насосов высокого давления (ТНВД) и форсунок, предложенных в 1898 году французом Сабатэ. Отказ от пневматического (компрессорного) впрыска был связан с тем, что на привод компрессора приходилось 10-15% полезной работы двигателя, в связи с чем расход топлива у таких дизелей был не совсем приемлемым, т.е. эффективные показатели были ниже, чем у цикла Сабатэ – Тринклера. Кроме того, гидравлический впрыск топлива позволял увеличить динамические показатели работы дизельного двигателя. Повсеместный переход от пневматического на механическое (бескомпрессорное) распыливание топлива и соответственно с цикла Дизеля на цикл Сабатэ — Тринклера начался в 30-х годах прошлого столетия. *** Цикл Сабатэ – ТринклераЦикл, включающий два последовательных термодинамических процесса сгорания топлива – сначала по изохоре, а затем по изобаре, называют циклом Сабатэ – Тринклера. Пожалуй, это название цикла тоже можно оспорить, поскольку французский инженер Сабатэ (Сабатье) запатентовал в 1898 году не цикл, а механическое устройство (форсунку с распылителем), которое должно было подавать жидкое топливо непосредственно в цилиндры в два этапа. По замыслу Сабатэ это должно привести к более полному и быстрому сгоранию топлива. В начале прошлого века российский инженер Густав Тринклер изобрел принципиально новый двигатель, опытный образец которого был изготовлен в 1902 году на Путиловском заводе. Снятая с работающего двигателя индикаторная диаграмма показала, что сгорание топлива в нем происходило по смешанному циклу – сначала по изохоре (при постоянном объеме), а затем по изобаре (при постоянном давлении). Термодинамические процессы в цикле Сабатэ – Тринклера осуществляется в следующей последовательности (см. диаграмму на рис. 1). Смешанный цикл в двигателе Тринклера имел место благодаря применению гидравлического впрыска топлива посредством форсунок, а также предварительному воспламенению топлива не в цилиндре, а в отдельной небольшой камере, соединенной каналом с объемом цилиндра. Именно в эту камеру бескомпрессорным (гидромеханическим) способом впрыскивалось топливо, где и начинался процесс его горения. Как упоминалось выше, все выпускающиеся в настоящее время дизельные двигатели на самом деле работают по циклу Сабатэ — Тринклера, т. е. циклу со смешанным подводом теплоты и с механическим распыливанием топлива. Степень сжатия у безнаддувных двигателей достигает значения 18-22; у наддувных высокофорсированных двигателей — 13-15. Область применения этих двигателей очень широкая. Их устанавливают в генераторных, насосных, энергетических установках и на электростанциях, в легковых и грузовых автомобилях, тракторах, сельскохозяйственной и дорожной технике, на тепловозах, судах, самолетах и т. д. *** Сравнение эффективности идеальных цикловПопробуем сравнить эффективность рассмотренных выше идеальных циклов с помощью диаграммы T-s (рис. 2), описывающей зависимость между энтропией и температурой рабочего тела. Анализ будет наиболее наглядным при одинаковых степенях сжатия в рассматриваемых двигателях (представим, что такое возможно). Из приведенной диаграммы (рис. 2б) видно, что процессы сжатия 1-2 у всех трех типов двигателей (карбюраторного, дизельного и бескомпрессорного) совпадают, а если отводить одинаковое количество теплоты, то будут совпадать и процессы 4-1. Следует отметить, что на диаграмме T–s изохора всегда проходит круче изобары, следовательно, в карбюраторном двигателе при одинаковом количестве подведенной теплоты будет совершаться больше работы на величину заштрихованной площади. Исходя из этого, можно сделать вывод: изохорное сжигание топлива эффективнее изобарного. Однако в действительности названные двигатели работают при разных степенях сжатия, и практический интерес представляет сравнение их эффективности при одинаковых максимальных температурах сгорания, поскольку именно они определяют в основном температурную напряженность машины и ее КПД. Следующая диаграмма T-s (рис. 2в) показывает циклы Отто, Дизеля и Сабатэ-Тринклера при одной и той же максимальной температуре. В этом случае на диаграмме T–s должны совпадать точки 3, что соответствует одинаковой максимальной температуре в цикле и одинаковому количеству отводимой за цикл теплоты. Здесь отрезки 1–2, 1–2′ и 1–2″ изображают адиабатное сжатие в циклах Отто, Дизеля и Сабатэ-Тринклера соответственно, 2–3 – изохорный подвод теплоты в цикле Отто, 2’–3 – изобарный в цикле Дизеля, 2″–3′ и 3’–3 – изохорный и изобарный в цикле Сабатэ-Тринклера. Остальные процессы – адиабатное расширение (рабочий ход) 3–4 и изохорный отвод теплоты 4–1 – при рассматриваемых условиях одинаковы для всех трех циклов. Как видно из этой диаграммы, максимальная теплота q0 (площадь, заключенная внутри контура цикла), преобразуемая в полезную работу и, следовательно, максимальный термодинамический КПД имеет место в случае цикла Дизеля, минимальный – в случае цикла Отто. Цикл Сабатэ-Тринклера по эффективности преобразования теплоты в полезную работу занимает промежуточное положение. Конечно, наиболее ценные результаты дает сопоставление циклов при одинаковых максимальных температурах и одинаковых расходах топлива (одинаковых количествах подводимой за цикл теплоты). Но сделать это с помощью диаграммы T–s практически невозможно, поскольку пришлось бы так подбирать количество отводимой теплоты, чтобы площади каждого из сравниваемых циклов были одинаковы. *** Термодинамика поршневого двигателя Скачать теоретические вопросы к экзаменационным билетам Скачать рабочую программу Скачать календарно-тематический план Главная страницаДистанционное образованиеСпециальностиУчебные дисциплиныОлимпиады и тестыЦикл ОттоС изохорным подводом теплоты. Рисунок 4.3. Диаграммы P-V и T – S цикла Отто (карбюраторный ДВС). Линия 1-2 – процесс адиабатного сжатия рабочего вещества ( смесь паров бензина и воздуха). Характеризуется: ε = V1/V2 = 6÷10. Это связано детонацией топлива Линия 2-3 –процесс изохорного подвода теплоты, (го- рение топлива внутри рабочей камеры). Характеризуется: λ = Р3/Р2 ≈ 2. Линия 3-4 – процесс адиабатного расширения продуктов сгорания ( обратный ход поршня). Линия 4-1 процесс изохорного отвода тепла. Цикл ДизеляС изобарным подводом теплоты. Рисунок 4.4 Цикл Дизеля. ( Диаграммы P-V и T-S). Линия 1- 2 – процесс адиабатного сжатия рабочего вещества, ( сжатие чистого воздуха). Характеризуется ε = V1/V2 = 13÷18. Линия 2-3 – процесс изобарного подвода теплоты ( впрыск топлива и горение топлива. Линия 3-4- процесс адиабатного расширения продуктов сгорания ( обратный ход поршня). Линия 4-1 – процесс изохорного отвода теплоты, (выпуск продуктов сгорания в атмосферу). Наиболее экономичным является двигатель внутреннего сгорания ДВС со смешанным подводом теплоты. Он имеет достаточно высокую степень сжатия ( как и цикл Дизеля) и работает на всех видах тяжелого топлива Недостатки ДВС.
В ДВС может применяться только жидкое и газообразное топливо, не дающее нагара и отложения смолы. 4.3 Устройство четырехтактного двигателя.На рисунке (4.5) схема четырехтактного карбюраторного двигателя (внешнее смесеобразование). Рисунок 4.5. Схема четырёхтактного карбюраторного ДВС. 1.Дроссельная заслонка; 2. Жиклер; 3. Поплавок; 4. Поплавковая камера; 5. Игла; 6. Топливный патрубок; 7. Отверстие в топливной камере; 8. Воздушный патрубок; 9. Воздушная заслонка; 10. Диффузор; 11. Распылитель; 12. Смесительная камера; 13. Впускной клапан; 14. Свеча ; 15. Выпускной клапан; 16. Цилиндр; 17. Поршень. 18. Кривошипно-шатунный механизм При движении поршня от внутренней мертвой точки М1 к наружной мертвой точке М2 в цилиндр всасывается смесь топлива (пары бензина) с воздухом под атмосферным давлением Р1 (линия е — а).Обратным движением поршня смесь адиабатно сжимается по линии а — b в результате чего повышается температура и давление до Р2,а объем уменьшается до объема камеры сгорания V0. Во внутренней мертвой точке ВМТ производится воспламенение от электроискры. Поскольку подготовленная смесь сгорает, быстро повышается до Р3 линия b — c. Образовавшиеся продукты сгорания расширяются по линии с-а, перемещая в точку НМТ. В точке М2 открывается, выхлопной клапан, через который газы под давлением Р4 вытекают в наружную среду. Отношение полного объема цилиндра к объему камеры сгорания называются степенью сжатия двигателя e: ; Полезная работа цикла равна разности подведенного и отведенного тепла: l0 = q1-q2; следовательно, термический К.П.Д. увеличивается с ростом степени сжатия e. Термодинамический анализ цикла ОттоТермодинамика это раздел физики, имеющий дело с энергией и работа системы. Он родился в 19 веке как ученые. впервые открыли, как строить и эксплуатировать паровые машины. Термодинамика имеет дело только с крупномасштабный ответ системы которые мы можем наблюдать и измерять в экспериментах. Как аэродинамики, нас больше всего интересует термодинамика двигательные установки а также высокая скорость потоков. На этой странице мы рассматриваем термодинамику четырехтактный внутреннее сгорание двигатель.Сегодня большинство самолетов гражданской авиации или частных самолетов с двигателем внутреннего сгорания (IC) , как и двигатель в вашем семейном автомобиле. Работа двигателя состоит из двух основных частей: механическая операция из детали двигателя, и термодинамика через который двигатель производит Работа а также сила. На этой странице мы обсуждаем основные термодинамические уравнения, которые позволяют для проектирования и прогнозирования характеристик двигателя. В двигателе внутреннего сгорания топливо и воздух воспламеняется внутри цилиндра.Горячий выхлоп толкает поршень, который соединен к коленчатый вал производить мощность. Сжигание топлива не является непрерывным процессом, но происходит очень быстро через равные промежутки времени. Между зажиганиями детали двигателя двигаться в повторяющейся последовательности, называемой циклом . Двигатель называется четырехтактным, потому что в нем четыре движения, или удары поршня за один цикл. На рисунке изображен сюжет давление против газа объем на протяжении одного цикла. Мы разорвали цикл на шесть пронумерованные этапы на основе механической операции двигателя.Для идеального четырехтактного двигателя впускной ход (1-2) а также ход выпуска (6-1) делаются при постоянном давлении и не способствуют генерации мощности двигателем. В течение ход сжатия (2-3), работа производится на газе поршнем. Если предположить, что тепло не поступает газа во время сжатия, мы знаем связи между изменением объема и изменением давления и температуры из наших решений уравнение энтропии для газа. Мы называем соотношение громкости в начале сжатие до объема в конце сжатия степень сжатия , r .(гамма — 1) где p — давление, T — температура, а гамма это соотношение удельные плавки. В течение процесс горения (3-4), объем поддерживается постоянным и выделяется тепло. Изменение температуры составляет данный Т4 = Т3 + f * Q / cv где Q — тепло, выделяемое на фунт топлива, которое зависит от топлива, f — соотношение топливо / воздух для сгорания, которое зависит от нескольких факторов. связанные с конструкцией и температурой в камере сгорания, и cv — удельная теплоемкость при постоянном объеме.(1 — гамма) Между этапом 5 и этапом 6 остаточное тепло переведен в окрестности так что температура и давление возвращаются к начальным условиям 1 этап (или 2). Во время цикла Работа производится на газе поршнем между ступенями 2 и 3. Работа выполняется газ на поршне между ступенями 4 и 5. Разница между работой, выполняемой газ и работа, проделанная с газом, показаны желтым цветом и являются произведенной работой по циклу. Мы можем рассчитать работу, определив прилегающую площадь по циклу на p-V диаграмме.Но поскольку процессы 2-3 и 4-5 кривые, это сложно. расчет. Мы также можем оценить работу W по разнице тепла в газ. минус тепло, отводимое газом. Зная температуры, это более простой расчет. W = cv * [(T4 — T3) — (T5 — T2)] Время работы, умноженное на скорость цикла (циклов в секунду cps ), равно в мощность P произведен двигателем. P = W * cps На этой странице у нас есть показан идеальный цикл Отто , в котором нет поступления тепла (или уходящий) газ при сжатии и силовых тактах, трения нет потери и мгновенное горение, происходящее при постоянном объеме.В действительности, идеального цикла не происходит, и есть много потерь, связанных с каждый процесс. Эти потери обычно учитываются коэффициентами эффективности. которые умножают и видоизменяют идеальный результат. Для реального цикла форма диаграммы p-V аналогичен идеальному, но площадь (работа) равна всегда меньше идеального значения. Деятельность: Экскурсии Навигация ..
1903 Термодинамический цикл двигателя — цикл ОттоБратья Райт использовали бензиновый, четырехтактный, двигатель внутреннего сгорания для питания своих самолет.В двигателе внутреннего сгорания топливо и воздух воспламеняется внутри цилиндр. Горячий выхлопной газ толкает поршень в цилиндр, который соединен с коленчатый вал производить мощность. Сжигание топлива не является непрерывным процессом, но происходит очень быстро через равные промежутки времени. Между зажиганиями детали двигателя двигаться в повторяющейся последовательности, называемой циклом . Двигатель называется четырехтактным, потому что в нем четыре движения. (штрихи) поршня за один цикл.Конструкция братьев была основана на ранних конструкциях автомобильных двигателей, в которых использовались Цикл Отто , разработанный немецким доктором Н.А. Отто в 1876 году. Дизайн братьев очень прост по сегодняшним меркам, так что это хороший двигатель для студентов, чтобы изучить основы работа двигателя. Работа двигателя состоит из двух основных частей: механическая операция частей двигателя и термодинамики, посредством которой двигатель производит Работа а также сила.На этой странице мы обсудим основные термодинамические принципы и на отдельной странице мы представляем термодинамический анализ что позволяет проектировать и прогнозировать характеристики двигателя. Термодинамика это раздел физики, имеющий дело с энергией и работа системы. Он родился в 19 веке как ученые. впервые открыли, как строить и эксплуатировать паровые машины. Термодинамика имеет дело только с крупномасштабным откликом системы. которые мы можем наблюдать и измерять в экспериментах.Основные идеи термодинамики преподаются в классах физики в средней школе. поэтому братья Райт знали и использовали эти концепции, особенно в своих конструкция двигателя. Мы разорвали цикл Отто на шесть пронумерованных этапов на основе механическая операция двигателя. На каждом этапе мы показываем разрез в цилиндре, чтобы выявить движение поршень и количество объема газа, создаваемого головкой поршень и цилиндр справа от головки поршня.На рисунке показан график давление по сравнению с объемом газа за один цикл. Цикл начинается в нижнем левом углу с Этап 1 является началом такт впуска двигателя. Давление близко атмосферное давление и объем газа минимальный, поршень далеко вправо в цилиндре. Между ступенью 1 и ступенью 2 поршень перемещается влево, давление остается постоянным, а объем газа увеличивается когда топливно-воздушная смесь всасывается в цилиндр через впускной клапан (красный). Этап 2 начинает такт сжатия двигателя с закрытие впускного клапана. Между этапом 2 и Стадия 3, поршень движется назад вправо, объем газа уменьшается, и давление увеличивается, потому что работа сделана на газ поршневой. Этап 3 — начало горение топливовоздушной смеси. Горение происходит очень быстро и объем остается постоянным. Высокая температура выделяется во время горения, что увеличивает как температура и давление, согласно уравнение состояния. Этап 4 начинает рабочий ход двигателя. Между этапом 4 и этапом 5, поршень возвращается влево, объем увеличивается, а давление падает как работа сделана по газу на поршне. На ступени 5 выпускной клапан (синий) открывается а остаточное тепло в газе равно обменялся с окружением. Громкость остается постоянным, а давление возвращается к атмосферным условиям. Этап 6 начинает такт выпуска двигателя, во время которого поршень сдвигается вправо, объем уменьшается и давление остается постоянным.В конце такта выпуска условия вернулись к этапу 1, и процесс повторяется. Во время цикла Работа производится на газе поршнем между ступенями 2 и 3. Работа выполняется газ на поршне между ступенями 4 и 5. Разница между работой, выполняемой газ и работа, проделанная с газом, показаны желтым цветом и являются произведенной работой по циклу. Время работы, умноженное на скорость цикла (циклов в секунду), составляет равно сила произведен двигателем.Площадь, ограниченная циклом на диаграмме p-V пропорциональна работе, произведенной в цикле. На этой странице у нас есть показан идеальный цикл Отто , в котором нет поступления тепла (или уходящий) газ при сжатии и силовых тактах, трения нет потери и мгновенное горение, происходящее при постоянном объеме. В действительности, идеального цикла не происходит, и есть много потерь, связанных с каждый процесс. Эти потери обычно учитываются коэффициентами эффективности. которые умножают и видоизменяют идеальный результат.Для реального цикла форма диаграммы p-V аналогичен идеальному, но площадь (работа) равна всегда меньше идеального значения. Деятельность: Навигация ..
Страница не найдена | MITПерейти к содержанию ↓
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов Предложения или отзывы? Термодинамические циклы: расчеты в ИнтернетеТермодинамические циклы: расчеты по Интернет А.Александров, К.А. Орлов, В.Ф. Очков (http://twt.mpei.ac.ru/ochkov) Московский Энергетический Институт (ТУ) (www.mpei.ru) Статья была опубликовано в журнале «Журмал вестник» МЭИ № 1, 2007 г. Английский редактирование Ричард Юшке Новое описаны подходы к расчету термодинамического цикла с использованием современных сетевые информационные технологии, которые могут изменить методы расчета и инструкция принципы теплотехники Сегодня математические пакеты [1] широко используются в образовании и инженерной практике. [1, 2], требующие пересмотра методики расчета и новой инструкции методы. Основная база расчетов в различных научных дисциплин (в частности, термодинамики) представляет собой набор формул и алгоритмы, которые были сформированы для ручных вычислений в докомпьютере (и даже в до калькулятора) эпохи [3]. Это налагает своего рода печать на формулы и методы их применение, которое препятствует их использованию в компьютерных вычислениях а также к пониманию студентами научной дисциплины. Формулы были часто чрезмерно упрощал .Более того, в множество формул, связанных с так называемыми технологическими причинами [4], т.е. методы и технические средства расчетов, используемые при выводе формул это не связано с его физической сущностью. Есть классический пример из термодинамика. На рис. 1 показан сайт в Интернете [2] , где с расчетом теплового КПД термодинамического цикла Отто, образованного двумя изохорными и двумя изоэнтропическими процессы.Некоторые люди помнят, как была разработана эта формула и что она правильно, если c p и c v (конкретные изобарические и изохорные теплоемкости рабочего тела) связаны с температурой. Это идеал случай, который не соответствует даже газу постоянного состава. В на самом деле рабочие вещества для электростанций представляют собой смеси с изменяющимися состав топливно-воздушных смесей, продуктов сгорания и др. Рисунок 1. Расчет теплового КПД
термодинамический цикл Отто по упрощенной формуле Возвращаясь к диссертации, отмеченной в начало статьи и подключение ее к расчетам термодинамического цикла, можно восстановить исходную формулу (точнее, набор формулы и алгоритмы). Современные математические системы (в частности Mathcad) может дать нам не только КПД цикла Отто, но и все промежуточные значения параметры рабочего тела в различных точках цикла. Рис. 2 показывает это расчет. Рисунок
2. Расчет теплового КПД цикла Отто по исходным формулам На рис.2 показано, что для расчета цикла Отто в Mathcad использовался встроенный оператор. Этот был определенным интегральным типом и блоком (Given-Find) для решения системы, в данном случае для системы интегрально-алгебраических уравнений. Эти инструменты позволяют нам вычислить основные соотношения термодинамики: уравнение Менделеева-Клапейрона PV = RT, интеграл по температуре и давление для расчета энтропии S, энтальпии H и интеграла по температуре для расчеты внутренней энергии U.Это дает возможность найти значения внутренняя энергия U вообще четыре точки цикла Отто и рассчитать эффективность цикла, используя эти ценности. На рис.2 видно, что постоянные c p и c v не вынимаются из интегралов. Для более сложных (настоящих) в расчетах можно подставить соответствующие функции одного (температуры), двух (температура и давление) или более (температура, давление, состав газа смесь) переменных для этих констант.Рис. 3 показывает расчет, в котором пользователь может выбрать рабочую среду, ее параметры (давление p 1 , температура T 1 , объемный степень сжатия r, максимальная температура T 3 ) и укажите оси диаграммы, визуализирующей цикл, или точку в цикле электростанция внутреннего сгорания. Рисунок 3. Расчет Отто
цикл, в котором теплоемкость рабочего тела зависит от температуры На рис. 3 показаны два диаграммы в конце расчета цикла Отто. Один из них обычный p, V-диаграмма (эту и другие диаграммы можно построить, выбрав соответствующий кнопки на осях). Другой — c p , p-диаграмма, которая представляет зависимость удельной изобарной теплоемкости рабочего тела (воздух, на рис.3) от температуры в пределах ее меняется в цикле Отто. В этом расчете пользователь может выбрать точку цикл: первая точка — начало процесса сжатия, точка 2 — конец сжатия, точка 3 — конец изохорного горения топливо-воздух смеси (здесь значения теплоемкости зависят от температуры и состава рабочего тела), а последняя точка 4 — конец хода поршня.Выбранная фаза определяет текущий кадр анимации [3] , выделенную точку на диаграмме и представленную параметры рабочего тела. В сетевом документе, показанном на рис. 3, расчеты рабочего вещества параметры выполняются не только для четырех точек, как показано на рис.2, но и для промежуточных точек с заданным шаг. Это позволяет нам создавать векторы, элементы которых являются параметрами рабочего вещества (p, T, v, s, h, U, c p и c v ), а также для построения графика объемные графики в различных системах координат (например, рис.6 ниже). Есть второе отличие расчетов, представленных на рис. 2 и 3. Рис. показаны расчеты на основе функций, предоставляемых пакетом WaterSteamPro [4] (www.wsp.ru) без использования отношения для идеального газа. Например, c p = aR, где a — постоянная связанные с составом газа. Пакет WaterSteamPro создан как инструмент для расчета теплопроводности воды и пара в программные языки C, Fortran, BASIC, Pascal, табличный процессор Excel и математический пакеты, такие как Mathcad, MatLab и т. д.Дополнительно список функций с префиксом wsp был увеличен и добавлены функции с префиксом wspg для расчеты термодинамических свойств отдельных газов и газовых смесей [5]. Это позволяет нам применять пакет WaterSteamPro для расчета пара. энергетические, газотурбинные, а также парогазовые [6]. Функции WaterSteamPro пакет доступен для использования в Интернете. Рис. 4 показывает Интернет [5] сайт, в котором пользователь может ввести значения в текстовые поля, нажмите кнопку Пересчитать и получить численные результаты значений энтропии, энтальпии и других свойства рабочего тела. Рисунок 4. Расчет параметров рабочего тела.
в энергетике технология Mathcad Calculation Server, дополнена авторской технологией доступа к расширенному списку встроенных функции числовой и символьной математики пакетов Mathcad и Maple, позволяет нам изменять образовательные сайты, связанные с теоретическими принципами теплотехники [7]. Вернемся к рисункам 13 и попробуем изменить постановку задачи, решаемой на этих сайтах. Цифры. 1 3 показывают, что a пользователь может изменить входные данные, отправить их на расчетный сервер (Mathcad Сервер вычислений), нажмите кнопку Пересчитать и получите новые результаты. в виде числовых данных, графиков и изображений. Технология Mathcad Calculation Server также дает нам возможность создавать сайты для распространения знаний, таких Что касается дистанционного обучения.На рис. 5 показан сайт. (верхняя часть), где посетитель (например, студент, решающий термодинамические проблема во время исследования) необходимо ввести формулы для правильного расчет теплового КПД цикла Отто и других параметров. Если формулы были введены правильно (int — интегральное, diff — дифференциальное и прочее здесь используется как обозначение и встроенные функции математических пакеты Mathcad и Maple, которые теперь стали стандартным человеком-компьютером интерфейс), затем значение в полях Ваш ответ и Правильный ответ (см. внизу часть рис.5) должен совпадать [6] . Рисунок 5. Сетевой шаблон и правильно заполненная сеть
шаблон задачи термодинамики Основная особенность представленного текстового задания на рис.5 и рис.6 состоит в том, что ученик должен работать с формулами, а не с числами. Много тестов системы требуют вычисления некоторых формул без ввода самой формулы.В качестве в результате часто невозможно определить, где были допущены ошибки: в расчетов или в подборе формул. Авторская методика тестирования сети. включая аналитическое преобразование и численные расчеты, позволяет студенту давать разные ответы. Например, варианты могут быть R * int (1 / p, р = р 0 р 1 ) или R * (p / p 0 ) или R * ln (p) R * ln (p 0 ). Кстати, последние два выражения неадекватно, если переменные p и p 0 имеют размер давления.Этот является результатом причин, упомянутых в начале статьи: попытка чтобы упростить вычисления и заменить деление вычитанием. Есть еще одна форма Интернет-образования. для теплоэнергетиков, как уже было сказано: продемонстрировано через трехмерная графика [7] . Рисунок 6. Трехмерный
графика цикла Ренкина Например, рис. 6 показывает диаграммы построенные на базе WaterSteamPro функции для цикла Ренкина. Мы можем сделать сеть вычисления как для скалярных значений, так и для векторов, т.е. с числом элементов исходных данных с помощью векторизации вычислений. На рис. 7 показан такой расчет и оптимизация. паровой установки с двумя подогревами. Рисунок 7. Расчет и
оптимизация цикла парогенератора с двумя ПП Используя Интернет-сайты, мы можем осуществлять расчеты эффективности цикла быстро и четко. Различные газы могут быть введенным в качестве рабочего тела. Например, мы можем определить, что для всех газы (за исключением одноатомных), тепловой КПД Отто цикл зависит от объемной степени сжатия, а также от максимальной температура газа. Таким образом, разница между тепловым КПД цикла и значения, рассчитанные по упрощенной формуле, могут составлять 5% и более.Очевидно, такая неточность в инженерных расчетах недопустима. студенты должны пройти обучение, чтобы избежать применения упрощенной формулы. это особенно важно учитывать зависимость КПД цикла от параметры рабочего тела в оптимизированных расчетах. Замена упрощенных формул на базовые алгоритмы расчетов (можно назвать расчетным ренессансом) позволяют нам вернуться от идеальных процессов к реальным. Другие расчеты термодинамических циклов доступно в Интернете: Лектор может показать зависимости эффективности различных термодинамических циклов во время лекций и семинаров с использованием сети расчеты.Соответствующие файлы Mathcad можно скачать с сайтов обсуждалось выше для их улучшения. Каталожные номера: 1. В.Ф. Очков. Сервер приложений Mathcad: Опыт эксплуатации в России // SoftLine Direct.2006, № 11, С.96. 98 2. В.Ф. Очков. Mathcad 14 для студентов и инженеры // СПб: БХВ-Петербург, 2007 3. А.А. Александров. Термодинамические принципы циклов электростанции // М.: Изд-во МЭИ, 2004, 158 с. 4. А.А. Александров, К.А. Орлов, В.Ф. Очков. Математические пакеты новый подход к расчетам в термодинамике и другие научные дисциплины // Изв. выс. учеб. зав. Проблемы энергетики. 2005, № 11-12, стр. 80-86 5. А.А. Александров, В.Ф. Очков, К. Орлов. Уравнения и программы для расчета свойств газов и горения. продукция // Теплотехника, 2005, Вып. 52, No 3, стр.28-37 6. А.А. Александров, К.А. Орлов, В.Ф. Очков. Исследование схем парогазовых установок с вдуванием пара в газ. поток на основе разработанных прикладных программ для свойств рабочих вещества ПГУ // Новое в российской электроэнергетике, 2004, № 4, С.28-37 7. В.Ф. Очков. Математическая пакеты и сетевой интерактивный справочник: проблемы и решения // Теплотехника, 2006, т. 53, № 6, С.71-77 Термодинамический цикл — Infogalactic: ядро планетарного знанияТермодинамический цикл состоит из связанной последовательности термодинамических процессов, которые включают передачу тепла и работу в систему и из нее, при этом изменяются давление, температура и другие переменные состояния внутри система, и это в конечном итоге возвращает систему в исходное состояние. [1] В процессе прохождения цикла рабочая жидкость (система) может преобразовывать тепло от теплого источника в полезную работу и отдавать оставшееся тепло в поглотитель холода, тем самым действуя как тепловой двигатель. И наоборот, цикл может быть обращен вспять и использовать работу для перемещения тепла от источника холода и передачи его в теплый сток, тем самым действуя как тепловой насос. Во время замкнутого цикла система возвращается в исходное термодинамическое состояние температуры и давления. Количества процесса (или количества пути), такие как тепло и работа, зависят от процесса.Для цикла, при котором система возвращается в исходное состояние, применяется первый закон термодинамики: Выше указано, что энергия системы не изменяется в течение цикла. E в может быть работой и подводимой теплотой во время цикла, а E из может быть работой и тепловыделением во время цикла. Первый закон термодинамики также диктует, что чистый подвод тепла равен чистому выходу работы за цикл (мы учитываем тепло, Q в , как положительное, а Q из как отрицательное).Повторяющийся характер технологического процесса позволяет работать в непрерывном режиме, что делает цикл важным понятием в термодинамике. Термодинамические циклы часто представляют математически как квазистатические процессы при моделировании работы реального устройства. Тепло и работаДва основных класса термодинамических циклов: энергетических цикла и тепловых циклов . Энергетические циклы — это циклы, которые преобразуют часть подводимого тепла в выходную механическую работу, в то время как циклы теплового насоса передают тепло от низких к высоким температурам, используя механическую работу в качестве входа.Циклы, полностью состоящие из квазистатических процессов, могут работать как циклы силового или теплового насоса, контролируя направление процесса. На диаграмме давление-объем (PV) или диаграмме температура-энтропия направления по часовой стрелке и против часовой стрелки указывают циклы мощности и теплового насоса соответственно. Отношение к работеЧистая работа равна площади внутри, потому что это (а) сумма работы Римана, проделанная над веществом из-за расширения, минус (б) работа, сделанная для повторного сжатия.Поскольку чистое изменение свойств состояния во время термодинамического цикла равно нулю, оно образует замкнутый контур на фотоэлектрической диаграмме.Ось Y PV диаграммы показывает давление ( P ), а ось X показывает объем ( V ). Область, ограниченная петлей, — это работа ( W ), проделанная процессом: Эта работа равна балансу тепла (Q), переданному в систему: Уравнение (2) делает циклический процесс похожим на изотермический процесс: даже несмотря на то, что внутренняя энергия изменяется в течение циклического процесса, когда циклический процесс завершается, энергия системы такая же, как энергия, которую она имела, когда процесс начался. . Если циклический процесс движется по контуру по часовой стрелке, то W будет положительным, и он представляет собой тепловую машину. Если он движется против часовой стрелки, то W будет отрицательным, и это будет тепловой насос. Каждая точка циклаОписание каждой точки термодинамических циклов.Цикл Отто: 1 → 2: Изэнтропическое расширение: постоянная энтропия (ы), снижение давления (P), увеличение объема (v), снижение температуры (T) 2 → 3: Изохорное охлаждение: постоянный объем (v), снижение давления (P), уменьшение энтропии (S), снижение температуры (T) 3 → 4: Изэнтропическое сжатие: постоянная энтропия (ы), увеличение давления (P), уменьшение объема (v), увеличение температуры (T) 4 → 1: Изохорный нагрев: постоянный объем (v), увеличение давления (P), увеличение энтропии (S), увеличение температуры (T) Список термодинамических процессов: Адиабатический: Отсутствие передачи энергии в виде тепла (Q) в течение этой части цикла составило бы δQ = 0.Это не исключает передачи энергии как работы. Изотермический: процесс находится при постоянной температуре в течение этой части цикла (T = постоянная, δT = 0). Это не исключает передачи энергии в виде тепла или работы. Изобарический: давление в этой части цикла остается постоянным. (P = константа, δP = 0). Это не исключает передачи энергии в виде тепла или работы. Изохорический: процесс имеет постоянный объем (V = постоянный, δV = 0). Это не исключает передачи энергии в виде тепла или работы. Изэнтропический: процесс с постоянной энтропией (S = константа, δS = 0). Это исключает передачу тепла, но не работает. Силовые циклыОсновная статья: Тепловой двигательТермодинамические энергетические циклы являются основой работы тепловых двигателей, которые поставляют большую часть мировой электроэнергии и приводят в движение подавляющее большинство автомобилей. Циклы питания можно разделить на две категории: реальные циклы и идеальные циклы. Циклы, встречающиеся в реальных устройствах (реальные циклы), трудно анализировать из-за наличия усложняющих эффектов (трения) и отсутствия достаточного времени для установления условий равновесия.Для анализа и проектирования создаются идеализированные модели (идеальные циклы); Эти идеальные модели позволяют инженерам изучать влияние основных параметров, определяющих цикл, без необходимости тратить много времени на проработку сложных деталей, присутствующих в реальной модели цикла. Циклы мощности также можно разделить в зависимости от типа теплового двигателя, который они хотят смоделировать. Наиболее распространенными циклами, используемыми для моделирования двигателей внутреннего сгорания, являются цикл Отто, который моделирует бензиновые двигатели, и цикл Diesel, который моделирует дизельные двигатели.Циклы, моделирующие двигатели внешнего сгорания, включают цикл Брайтона, который моделирует газовые турбины, цикл Ренкина, который моделирует паровые турбины, цикл Стирлинга, который моделирует двигатели горячего воздуха, и цикл Эрикссона, который также моделирует двигатели горячего воздуха. Указанный стрелками термодинамический цикл по часовой стрелке показывает, что цикл представляет собой тепловую машину. Цикл состоит из четырех состояний (точки показаны крестиками) и четырех термодинамических процессов (линии).Например, выходная механическая работа «давление-объем» из цикла тепловой машины (чистая выработка), состоящего из 4 термодинамических процессов, составляет [ цитата необходима ] [ сомнительно — обсудить ] : Если в процессе 4-1 и 2-3 не происходит изменения объема, уравнение (3) упрощается до: Циклы теплового насосаОсновная статья: Тепловой насос и холодильный циклТермодинамические тепловые насосы являются моделями бытовых тепловых насосов и холодильников.Между ними нет разницы, за исключением того, что целью холодильника является охлаждение очень небольшого помещения, в то время как бытовой тепловой насос предназначен для обогрева дома. Оба работают, перемещая тепло из холодного помещения в теплое. Наиболее распространенный цикл охлаждения — это цикл сжатия пара, который моделирует системы, в которых используются хладагенты с изменяющейся фазой. Абсорбционный холодильный цикл является альтернативой, при которой хладагент поглощается в жидком растворе, а не испаряется. Циклы охлаждения газа включают в себя обратный цикл Брайтона и цикл Хэмпсона-Линде.Множественные циклы сжатия и расширения позволяют газовым холодильным установкам сжижать газы. Моделирование реальных систем
Термодинамические циклы могут использоваться для моделирования реальных устройств и систем, как правило, с помощью ряда предположений. [2] упрощающие предположения часто необходимы, чтобы свести проблему к более управляемой форме. [2] Например, как показано на рисунке, такие устройства, как газовая турбина или реактивный двигатель, могут быть смоделированы как цикл Брайтона. Настоящее устройство состоит из серии этапов, каждая из которых моделируется как идеализированный термодинамический процесс. Хотя каждая ступень, которая воздействует на рабочую жидкость, представляет собой сложное реальное устройство, их можно смоделировать как идеализированные процессы, которые приблизительно соответствуют их реальному поведению. Если энергия добавляется другими способами, кроме сжигания, то дополнительное предположение состоит в том, что выхлопные газы будут проходить от выхлопа к теплообменнику, который отводит отработанное тепло в окружающую среду, а рабочий газ будет повторно использоваться на входной ступени. Разница между идеализированным циклом и фактической производительностью может быть значительной. [2] Например, следующие изображения иллюстрируют различия в производительности, предсказанной идеальным циклом Стирлинга, и фактическими характеристиками двигателя Стирлинга:
Поскольку чистый выход работы для цикла представлен внутренней частью цикла, существует значительная разница между прогнозируемым выходом работы идеального цикла и фактическим выходом работы, показанным реальным двигателем.Также можно заметить, что реальные индивидуальные процессы расходятся с их идеализированными аналогами; например, изохорное расширение (процесс 1-2) происходит с некоторым фактическим изменением объема. Известные термодинамические циклыНа практике простые идеализированные термодинамические циклы обычно состоят из четырех термодинамических процессов. Могут использоваться любые термодинамические процессы. Однако при моделировании идеализированных циклов часто используются процессы, в которых одна переменная состояния поддерживается постоянной, например изотермический процесс (постоянная температура), изобарический процесс (постоянное давление), изохорный процесс (постоянный объем), изэнтропический процесс (постоянная энтропия). , или изэнтальпийный процесс (постоянная энтальпия).Часто также используются адиабатические процессы, при которых теплообмен не происходит. Вот некоторые примеры термодинамических циклов и составляющих их процессов: Идеальный циклИллюстрация идеального цикла теплового двигателя (стрелки по часовой стрелке).Идеальный цикл состоит из:
Внутренняя энергия идеального газа в различных частях цикла: Изотермический: Изохорная: Изобарический: Цикл КарноОсновная статья: цикл КарноЦикл Карно — это цикл, состоящий из полностью обратимых процессов изоэнтропического сжатия и расширения и изотермического добавления и отвода тепла.Тепловой КПД цикла Карно зависит только от абсолютных температур двух резервуаров, в которых происходит теплопередача, и для энергетического цикла составляет: где — самая низкая и самая высокая температура цикла. Для энергетических циклов Карно коэффициент полезного действия теплового насоса составляет: ., а для холодильника КПД: .Второй закон термодинамики ограничивает КПД и COP для всех циклических устройств до уровней, равных КПД Карно или ниже.Цикл Стирлинга и цикл Эрикссона — это два других обратимых цикла, в которых для получения изотермической теплопередачи используется регенерация. Цикл СтирлингаОсновная статья: цикл СтирлингаЦикл Стирлинга похож на цикл Отто, за исключением того, что адиабаты заменены изотермами. Это также то же самое, что и цикл Эрикссона с изобарическими процессами, заменяющими процессы постоянного объема.
Тепло течет в петлю через верхнюю изотерму и левую изохору, и часть этого тепла течет обратно через нижнюю изотерму и правую изохору, но большая часть теплового потока проходит через пару изотерм.Это имеет смысл, поскольку вся работа, выполняемая циклом, выполняется парой изотермических процессов, которые описываются как Q = W . Это говорит о том, что все чистое тепло проходит через верхнюю изотерму. Фактически, все тепло, которое поступает через левую изохору, выходит через правую изохору: поскольку верхняя изотерма имеет одну и ту же более высокую температуру, а нижняя изотерма имеет одну и ту же более низкую температуру, и поскольку изменение энергии для изохора пропорциональна изменению температуры, тогда все тепло, поступающее через левую изохору, компенсируется именно теплом, выходящим из правой изохоры. Функции состояния и энтропияЕсли Z является функцией состояния, то сальдо Z остается неизменным во время циклического процесса:
Энтропия является функцией состояния и определяется как , так что
тогда понятно, что для любого циклического процесса означает, что чистое изменение энтропии за цикл равно 0. См. ТакжеPPT — Термодинамические циклы Презентация PowerPoint, скачать бесплатноТермодинамические циклы • Цель • Классификация термодинамических циклов • Анализ и расчет термодинамических циклов • Цикл паров Карно, цикл Рэнки, цикл регенерации, цикл повторного нагрева газа Рэнки • Когенерация Цикл охлаждения • Цикл паро-компрессионного охлаждения • Хладагент • Другие циклы охлаждения Классификация циклов термодинамики Цикл питания (+) Тепловая энергия Механическая энергия Цикл теплового насоса (-) Цикл охлаждения: поддерживайте низкую температуру источника тепла с низким температура Цикл теплового насоса: поддержание высокой температуры источника тепла с высокой температурой Цикл рабочего тела и газа: отсутствие фазового перехода рабочего тела во время цикла Цикл пара: изменение фазы рабочего тела во время цикла Форма сгорания Паровой цикл Карно С этим циклом связано несколько непрактичных cle: 1.Нецелесообразно проектировать компрессор, который будет обрабатывать две фазы процесса изоэнтропического сжатия (4-1). 2. В процессе изоэнтропического расширения (2-3) снижается качество пара, что приводит к повреждению лопаток турбины. Цикл паров Карно 3. Критическая точка ограничивает максимальную температуру, используемую в цикле, что также ограничивает термический КПД. 4. Удельный объем пара намного выше, чем у воды, что означает большой объем работы и затрат оборудования. S 6 1 4 2 3 Цикл пара Ренкина 4-6 Подвод тепла при постоянном давлении в котле 6-1 к перегретому пару 1-2 Изэнтропическое расширение в турбине 2-3 Отвод тепла при постоянном давлении в конденсаторе 3 -4 Изэнтропическое сжатие в насосе p S 6 p1 1 4 5 6 1 4 p2 3 2 v T 2 1 5 3 6 4 2 3 с Цикл пара Ренкина Тепловая эффективность пара Ренкина Цикл 4-5-6-1 Подвод тепла при постоянном давлении в котле 1-2 Изэнтропическое расширение в турбине 2-3 Отвод тепла при постоянном давлении в конденсаторе 3-4 Изэнтропическое сжатие в насосе Тепловой КПД Цикл паров Ренкина 1.Жесткая сжимаемость воды 2. Ek, Ep = 0 Термическая эффективность цикла паров Ренкина Определение: d (汽 耗 率) — скорость тепла, необходимая для создания работы Повышение эффективности пара Ренкина Цикл 1 ‘ 1 5′ 5 4 3 2 ‘2 Повышение эффективности цикла паров Ренкина 1. — Давление пара на входе в турбину - Измените два цикла: ① 3-4-5-1-2- 3 ② 3-4-5′-1′-2’-3 1 ‘ 1 5′ 5 4 3 2 ‘2 Повышение эффективности цикла паров Ренкина Недостатки: 1.Присутствие большого количества влаги очень желательно, поскольку оно снижает КПД турбины и разрушает лопатки турбины. Повышение требований к инвестициям в сосуды под давлением и оборудование. 2. 1 ‘ 1 5 6 4 3 2 2′ Повышение эффективности цикла паров Ренкина 2. — Температура пара на входе в турбину - Замена двух циклов: ① 3-4-5-6-1-2 -3 ② 3-4-5-6-1′-2′-3 1 ‘ 1 5 6 4 3 2 2′ Повышение эффективности цикла паров Ренкина Преимущества: i ii перегрев пара до более высокой температуры желательно, потому что он снижает влажность пара на выходе из турбины.Недостатки: температура перегрева ограничена металлургическими соображениями. 1 6 5 4 4 ‘2 3 3’ 2 ‘Повышение эффективности цикла паров Ренкина 3. — Давление в конденсаторе, выход из турбины - Замена двух циклов: ① 1-2-3-4-5-6- 1 ② 1-2′-3′-4’-5-6-1 1 6 5 4 4 ‘2 3 3’ 2 ‘Повышение эффективности цикла паров Ренкина i Недостатки: ii i Давление конденсации составляет ограничивается давлением насыщения, соответствующим температуре.ii Это увеличивает содержание влаги, что крайне нежелательно. Повышение эффективности парового цикла Ренкина Пример • Рассмотрим паровую электростанцию, работающую на идеальном цикле Ренкина. • Пар поступает в турбину при 2,5 МПа и 350 ℃ и конденсируется • в конденсаторе под давлением 70 кПа. Определите • Тепловой КПД этой электростанции • Тепловой КПД, если пар конденсируется при давлении 10 кПа • Тепловой КПД, если пар перегрет до 600 ℃ • Тепловой КПД, если давление в котле повышается до 15 МПа • При температуре на входе в турбину поддерживается при 600 ℃ 3 2.5 МПа 2 70 кПа 1 4 Состояние 1: Состояние 2: Идеальное состояние цикла Ренкина 3: 3 2,5 МПа 2 70 кПа 1 4 Состояние 4: Состояние 1: Состояние 2: (b) Понижение давление конденсатора Состояние 3: 2,5 МПа Состояние 4: Фактический цикл паров Ренкина Необратимость • Трение жидкости • Теплопередача под температурой • разница • Потери тепла в окружающую среду 1 5 6 3 (4) 2 2 ‘Фактический КПД турбины с паровым циклом Ренкина Идеальный цикл Фактический цикл Фактический паровой цикл Ренкина Механический КПД Относительный КПД Эффективный КПД энергетического котла КПД оборудования T 1 6 5 7 2 3 (4) eds Ideal Regenerative Cycle 预热 锅炉 给水 , 温度 升高 后再 进入 锅炉 可 锅炉 的 的 平均 吸热 温度 , 减小 水 与 热源 , 提高有利。 the 汽轮机 中 的 蒸汽 预热 锅炉 给水 称为 回 热。 Передача тепла питательной воде от бывшей выброс пара в теплообменник, встроенный в турбину, называется регенерацией.Регенеративный цикл: 1-7-d-3-4-5-6-1 Общий цикл Карно: 3-4-5-7-d-3 Идеальный цикл Карно: 5-7-2-e-5 Одинаковая эффективность 1 Турбинный котел 7 2 Регенератор Конденсатор камеры смешения 4 6 5 3 Насос II Насос I Идеальный цикл регенерации Откачивающая регенерация T 1 1 кг 6 акг 7 5 (1-а) кг 3 (4) 2 s Идеальный цикл регенерации> 0 T 1 9 8 6 7 4 5 3 2 s Идеальный цикл регенерации 1 Турбинный котел Регенератор 7 2 Смесительная камера 8 Конденсатор 9 4 6 5 3 Насос II Насос I Идеальный цикл повторного нагрева 蒸汽 经 汽轮机 绝热 至 中间 压力 时 全部 中 中 特设 的 再 加热器 中 再 温度 升高 后再 全部 引入 汽轮机。 1 a 5 b 6 4 3 c 2 Промежуточное давление идеального цикла повторного нагрева Когенерация • Определение • Когенерация — это производство более чем одного • полезного вида энергии из одного источника энергии.• электроэнергия • низкое качество тепла 背压 式 热电 联 供 抽气 式 供 Цикл охлаждения газа Идеальный обратный цикл Карно T1 — Температура источника тепла с высокой температурой, окружающей температурой T2 — Температура тепла источник с низкой температурой, источник холода q1 — Тепло, отводимое в окружающую среду q2 — Тепло, поглощаемое от источника холода w0 — Потребляемая мощность Конденсатор 3 2 Турбина компрессора 1 4 Цикл охлаждения холодного газа источника 1-2 Изотропный компрессор 2- 3 Отвод изотонического тепла в окружающую среду 3-4 Изотропное расширение 4-1 Изотоническое поглощение тепла p 3 2 4 1 v T 2 3 T3 T1 1 4 с Цикл охлаждения газа Cp — постоянный, идеальный газ • Поглощение тепла от Источник холода • Тепло, отбрасываемое в конденсатор • Работа компрессора • Работа турбины Цикл охлаждения газа Цикл охлаждения газа 9 0005 Цикл парокомпрессионного охлаждения • Недостатки газокомпрессионного цикла охлаждения • 1.небольшой коэффициент охлаждения, поскольку поглощение и отвод тепла не являются изотермическими процессами; • 2. Низкая холодопроизводительность хладагента (газа) • Итак… хладагент заменяется на пар • Наивысший КПД имеет обратный цикл пара Карно. Непрактичность: 1. Большое содержание влаги крайне нежелательно для компрессора и турбины. 2. Производительность ограничена расширением жидкости в турбине. Цикл парокомпрессионного охлаждения • Итак… практический цикл парокомпрессионного охлаждения: 2 2 3 4 3 4 1 1 6 5 2 4 3 1 6 5 Цикл парокомпрессионного охлаждения 2 4 3 1 6 5 Дроссель паро-компрессионного цикла охлаждения: ① жидкость низкого качества трудно сжимать.② рабочие потери относительно невелики ③ легко регулировать давление жидкости и температуру источника холода. Разница в работе между турбиной и дросселем Цикл паро-компрессионного охлаждения Регенерация — более реалистичный цикл Преимущества: 1. |

